世界上谁先证明了勾股定理，毕达哥拉斯还是商高？

中学时我们都学过，勾股定理又叫毕达哥拉斯定理，西方认为是毕达哥拉斯首先证明了勾股定理。

据《周髀算经》记载，中国古代学者早在周朝早期就发现了勾股定理。

商高曰：“数之法出于圆方，圆出于方，方出于矩，矩出于九九八十一。故折矩，以为句广三，股修四，径隅五。既方之，外半其一矩，环而共盘，得成三四五。两矩共长，二十有五，是谓积矩。故禹之所以治天下,此数之所生也。————《周髀算经》

由于，这段对话发生在商高和周公之间。所以，有人认为早在周朝早期，公元前11世纪，商高就发现了勾股定理。比毕达哥拉斯早了500年。

国内学者研究普遍认为，《周髀算经》成书在西汉，不早于公元前1世纪，书中这段对话为后人托商高之名伪作。也有学者认为，虽然成书在西汉，但是看内容应该是不同人，在不同时期记录内容的累积。关于商高的部分也可能是早期记录流传下来的。

不过即使认定《周髀算经》记录的商高的对话属实，由于书中没有给出勾股定理的严格演绎证明。不能据此说商高证明了勾股定理，只能说是中国很早就发现了勾股定理的一个特例。

严格证据上来看，最早发现勾股定理的是古代巴比伦。在公元前16～19世纪之间，古巴比伦人留下的泥石板上记载了多组勾股数。比毕达哥拉斯早了1000多年。

毕达哥拉斯证明勾股定理的证据，来自于古希腊人普罗克鲁斯为欧几里得的《几何原本》的评论中：

如果我们相信那些愿意调查古代历史的人所说的，也许会发现，他们把这个定理归于毕达哥拉斯，并说他为了庆祝这个发现，杀了一头牛来献祭。

普罗克鲁斯据说生活在公元五世纪，比毕达哥拉斯晚了1000年，而毕达哥拉斯的具体证明方法没有流传下来。从严格证据角度来说，不能认为毕达哥拉斯最早证明了勾股定理。

世界上明确记录了勾股定理的证明方法，最早的书是欧几里得的《几何原理》。

中国正式有记录的勾股定理的证明，来自于三国时期的赵爽。他在为《周髀算经》作注时给出了证明。比公元前300年的《几何原理》晚了大约500年了。

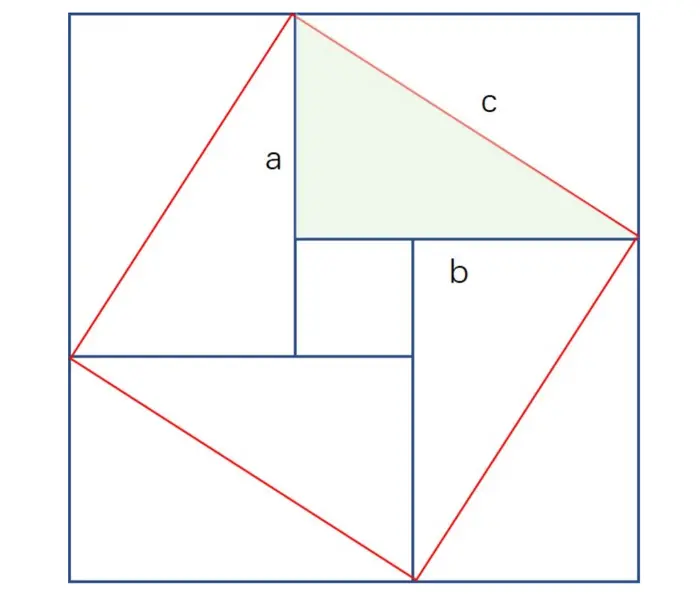
外面正方形的面积等于里面4个直角三角形面积加上中间小正方形的面积，也就是：
c² = (ab / 2) * 4 + (a-b)² = 2ab + a² - 2ab + b² = a² + b²

由于《几何原理》提供的证明方法成熟，而且相对复杂，更像是处于编写教材的需要采纳了一个相对复杂的证明方法。而在比毕达哥拉斯更早的时代，古希腊学者就使用了演绎法证明几何问题。所以普遍认为，在《几何原理》成书之前，古希腊人已经知道勾股定理的证明方法。

而由于中国古代数学重计算轻证明，重实用轻理论。我们很难把赵爽的证明前推到更早的时期。

很多学者更是认为就是因为中国古代数学重计算轻证明的特点，阻碍了近代科学的产生。