中国古代如何测量天的高度?和古希腊差距在哪里?
在古希腊人测算日、月的大小和距离的时候。中国古代也对太阳的大小,太阳到地面的距离进行了测算。
根据《周髀算经》的记载,古代测算出太阳的直径为1250里,太阳到地面日下无影处的距离为8万里。
实际上太阳到地球的平均距离是14960万公里,太阳直径是139万公里。
中国古代这个和古希腊测算结果相比,数据准确度要离谱的多。
造成差距的直接原因有两点:
- 测量方法错误
- 测量行为太粗略
中国古代测量太阳距离和大小的方法
根据《周髀算经》,首先利用日影测量太阳到地面的距离。
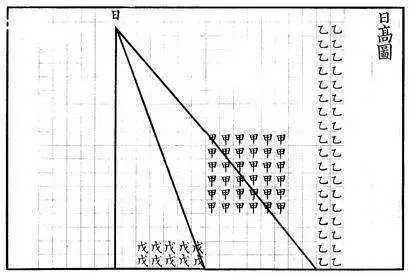
把8尺长的竹竿竖在周王城中一块空地上,当作“表”(也称“髀”);可以观察到,在每年夏至日正午,表的日影最短,为1尺6寸;并且朝着正南(北)方向,每过1000里,表影就短(长)1寸。于是,在表影长为6尺的那天正午,表正南6万里处日下无影。
然后运用勾股定理和比例方法算出,太阳到地面日下无影处的距离为8万里,太阳到王城观测点的距离为10万里。
知道了太阳和地面的距离,利用“竹空测日”测量太阳直径。
用长8尺(当时的1尺约合23厘米)的空心竹竿对准太阳,则在竿的一端观察到太阳正好掩住竿另一端的中孔,由此得到:
太阳到地面观察点的距离/太阳直径 ≈ 竹竿长度/孔径 ≈ 80
太阳的直径 ≈ 太阳到地面观察点的距离 / 80
于是进一步算出,太阳的直径为1250里。
由于地球是球体,太阳距离地面非常远,这种利用日影和三角函数的方法是不可能测量出太阳到地面的距离的。
由于中国古代不知道地球是球体,也不知道太阳距离地面非常远。把地面简单当成了平面,把太阳直接简化成了点光源。所以错误的认为这种方法能测出太阳到地球的距离。
从记录的数据看,千里一寸、8尺竹杠掩住中孔,应该是没有经过细致实测验证形成的结果。
古希腊埃拉托色尼利用日影测量地球周长
由于地球是球体,通过日影不能测出太阳的距离,但是可以测出地球的周长。
埃拉托色尼选择同一经线上的两个地点:赛因(在今天的阿斯旺)和亚历山大港,在夏至日那天测量亚历山大港物体影子的长度。
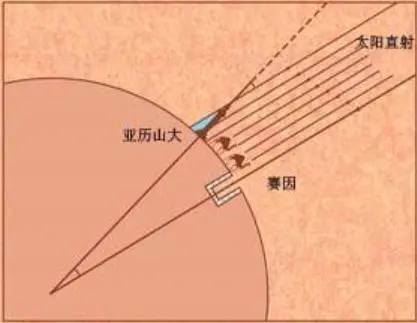
由于已知赛因在夏至日当天,太阳可以照进井里没有影子。因此,当天物体和影子构成三角形的夹角就是亚历山大港、赛因的地球弧长对应的夹角。
赛因和亚历山大港的距离 / 夹角的度数 * 360 = 地球的周长。
当天测出的夹角是7°12′,大约是360°的1/50。因此:
地球的周长 ≈ 赛因和亚历山大港的距离 * 50
据测测算出地球的周长是39690公里,和现在的通用值40000公里很接近。
阿利斯塔克利用日食与月食,测量太阳、月亮距离和大小
月球从地平线上升起要花费大约两分钟的时间。地球自身旋转360°要用上一天的时间,而转动一个月球的周长则只需花费两分钟。那么月球直径应该占据了大约0.5°的月球绕地轨道。
2 / (24 * 60) * 360° ≈ 0.5°
在一次月食中月球停留在地球阴影中的时间最多可达三个小时。月球绕地球运行一周需要一个月的时间,需要三个小时通过地球的阴影带,因此推算出地球的阴影占据了大约1.5度的月球绕地轨道。
3 / (24 * 30) * 360° ≈ 1.5°
因此,地球的直径大约是月亮的直径的三倍:
地球直径 / 月亮直径 ≈ 1.5° / 0.5° ≈ 3
根据这个弧度关系还可以计算地月距离和地球直径的比值:
月球绕地轨道周长 = 地月距离 * 2π ≈ 地球直径 * 360° / 1.5°
地月距离 / 地球直径 ≈ 360° / 1.5° / 2π ≈ 40
由于事实上太阳不是一个点光源,而是一片光区。太阳所投射到月轨道的阴影,并不是一个完整的地球,而是地球直径的四分之三的长度。据此,修正下原来的计算结果:
月亮直径 / 地球直径 / ≈ (1 / 3) * (3/4) ≈ 1 / 4
地月距离 / 地球直径 ≈ 40 * (3/4) ≈ 30
阿里斯塔克斯意识到,当我们看到上弦月的时候,地球、月亮和太阳三者形成了一个直角三角形,如图所示。
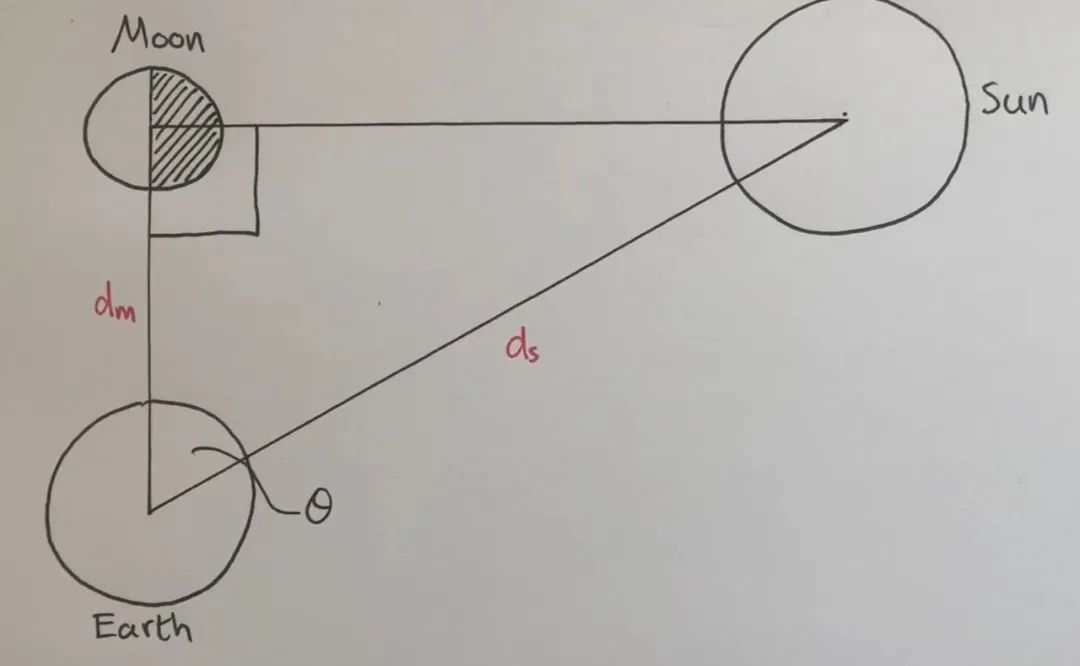
如果我们能测量出图中的θ角,那么我们也就能计算出日地距离与地月距离的比例。
地月距离 / 地日距离 = cosθ
当时测出来θ角是87°,现在的测试结果为89.853°,由于这个角度太接近90°,2°多的误差导致距离比的误差放大了很多倍。当时测出的结果是日地距离是地月距离的19倍。
由于日食时,月亮和太阳看起来一样大。既然日地距离是月地距离的19倍。那么太阳直径应该是月亮直径的19倍。
太阳直径 / 月亮直径 = 日地距离 / 地月距离 = 19
当时阿利斯塔克利实际测算的结果,地球的直径是月亮的直径的2.85倍,地月距离的距离是地球直径的20倍,日地距离是地球直径的380倍,太阳直径是地球直径的6.7倍。现代这几个数据测量结果是3.5,30,11760,109。
喜帕恰斯使用阿利斯塔克的方法,测得地月距离的距离是地球直径的30倍。这是之后一千九百年间,人们所知离地球有多远的唯一天体。
古希腊测算结果虽然误差也很大,由于采用的方法理论上是正确的,测算数据比中国古代的测量结果好太多了。两者差距的关键在于中国古代尝试测试太阳高度使用了错误的事实作为假设:
- 大地是平的。
- 太阳是点光源。